We cannot understand the history of the Earth or the evolution of life without measuring time. In this chapter we’ll see how scientists use different types of rocks to measure both relative and absolute ages, and ultimately the age of the Earth itself.

The Rock Cycle

Geologists classify into three major groups according to how they form.

• Igneous rocks are made from molten magma or lava that solidifies into rock. The chemical compositions of the magma and the rate at which it cools determine the type of rock formed. Igneous rocks include granite and basalt.
• Sedimentary rocks are layered rocks formed when sand and silt collect on the surface or in bodies of water and cement together to form new rock. Examples include sandstone and shale.
• Metamorphic rocks form when rocks undergo temperatures and/or pressures that are high enough to cause structural or chemical transformations without melting them entirely. Marble and slate are metamorphic rocks.

Over geological time, different types of rocks can transform into one another, in a process called the rock cycle (Figure 1). For example, metamorphic or sedimentary rocks can be melted and transformed into igneous rocks, and all three rock types can be eroded into sediments that form new sedimentary rocks. Heat and pressure can transform igneous and sedimentary rocks into metamorphic rocks. Sedimentary and igneous rocks are most useful for measuring ages, as we’ll see below.

Relative Dating with Sedimentary Rocks

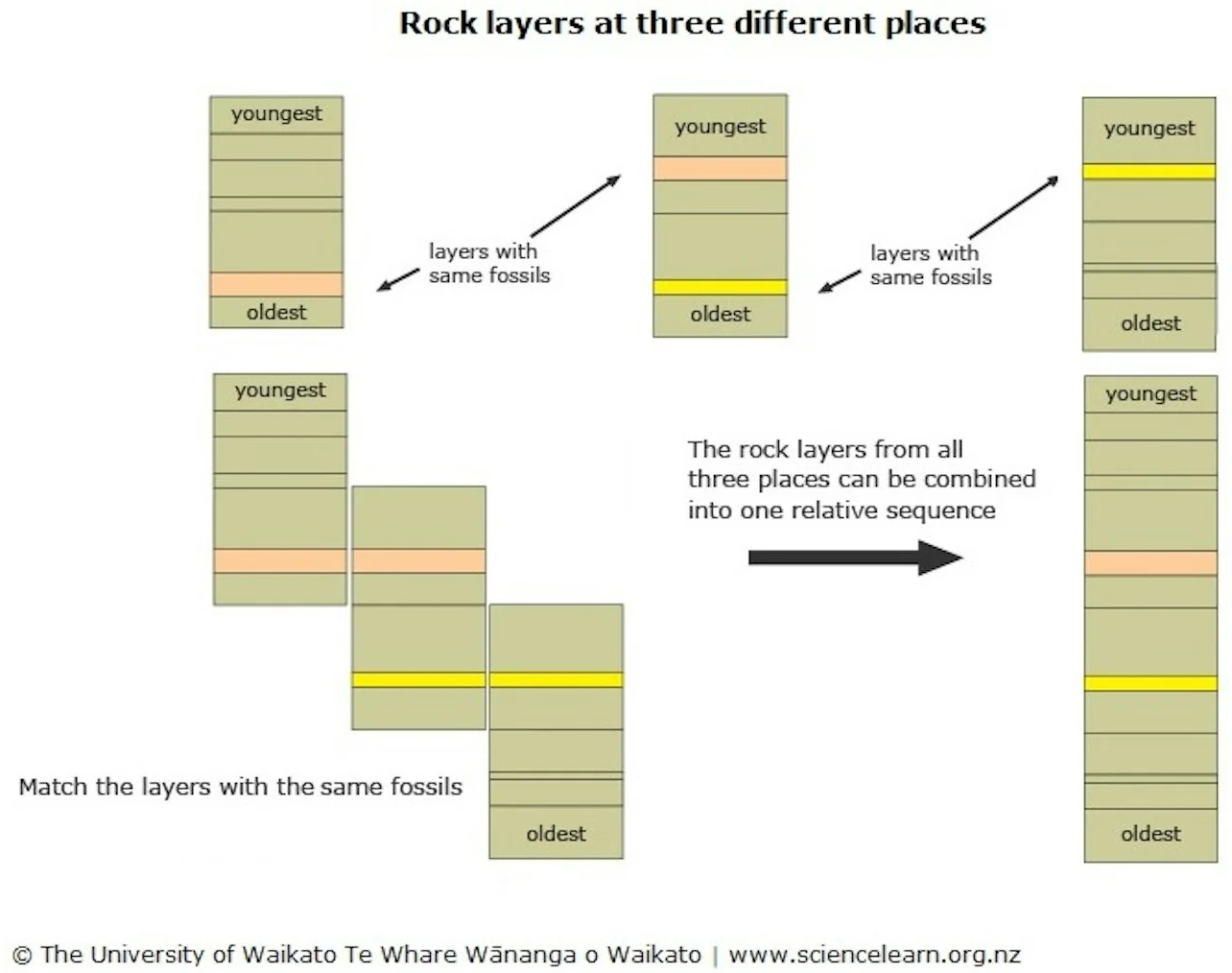
Because sedimentary rocks are gradually deposited in layers over time, most fossils are preserved in sedimentary rocks. The presence sof fossils and the process of gradual deposition makes these rocks particularly valuable for the study of the history of the Earth. Sedimentary layers (called strata) enable relative dating: the process of determining if one rock or geologic event is older or younger than another, without knowing their actual ages.

Relative dating is based on a number of principles, the most fundamental of which is that in an undisturbed sequence of sedimentary strata, the oldest layers are on the bottom and the layers above are younger. This is a consequence of the deposition of sediments over time. Fossils can then be used to align sedimentary strata from different locations. Unlike (most) types of rock, living organisms appear for a while in the fossil record and then go extinct, so fossils of the same type in rocks from different regions have roughly the same ages. By matching layers with the same fossils, scientists can combine strata from many locations to construct a relative sequence. This is how the geological timescale was initially constructed.

Radiometric Dating

As we’ve seen, sedimentary rocks are extremely valuable for determining relative ages and constructing a timeline, but they can’t tell us how many millions or billions of years ago a rock was formed. To figure that out, we take advantage of the process of radioactive decay.

Radioactive Decay

The absolute ages of certain types of rocks can be determined by a process known as radiometric dating. First described in 1907 by Bertram Boltwood, this method is now widely used for dating specimens throughout geology and uses known properties of atomic physics.

Recall that all the matter that we interact with every day is made up of protons, neutrons and electrons, and that atoms can exist as several different isotopes, which contain different numbers of neutrons in their nucleus. Not all nuclei are stable. Generally, heavier isotopes with an unbalanced number of neutrons relative to protons will undergo radioactive decay. For example, all carbon atoms have 6 protons, but different numbers of neutrons are possible: carbon-12 and carbon-13 are stable isotopes, but carbon-14 is an unstable isotope. The unstable isotopes (here, carbon-14) are known as parent isotopes, and they spontaneously decay into a different element or isotope, known as the daughter isotope.

There are two different types of statistically predictable spontaneous decay. The first is known as alpha decay (Figure 3 below), so named because the process emits an alpha particle (two protons and two neutrons). Alpha decay can only occur with very large nuclei. The parent isotope is left with a reduction of four in atomic mass. The loss of two protons means that the parent isotope has been converted to a lighter element in the periodic table.

A second type of spontaneous decay is beta decay. The atomic mass (total number of protons + neutrons) remains the same, but the atomic number (number of protons) changes. A proton or neutron may change into the other by flipping the charge of one quark (protons and neutrons are made of quarks).  With [latex]\beta ^-[/latex] decay, a neutron decays into a proton plus an electron (to maintain charge balance) and an electron antineutrino to carry away energy. This changes the atom to a heavier element (it gains one proton). An example of [latex]\beta ^-[/latex] decay is the conversion of ¹⁴C (6 protons) to ¹⁴N (7 protons):

                    [latex]^{14}_6C \rightarrow \ ^{14}_7 N + e^- + \nu_e[/latex]

With [latex]\beta ^+[/latex] decay, the proton becomes a neutron, absorbing an electron, and the atom is changed to a lighter element (it loses one proton). And example of [latex]\beta ^-[/latex] decay is conversion of magnesium (12 protons) to sodium (11 protons):

                   [latex]^{23}_{12} Mg \rightarrow ^{23}_{11}Na + e^+ + \nu_e[/latex]

It is impossible to say for sure when a decay event will happen, but we can categorize the rate at which a sample of atoms will decay. If we know the amount of parent and daughter isotope, then knowing the rate of decay allows us to solve for how much time it must have taken for the parent isotope to decay into that much daughter isotope. This rate is characterized by the half-life, or the amount of time it takes for half of the parent isotope to decay into the daughter isotope. Different elements have different half-lives, and so are useful for dating different age ranges. The table below lists decay information for common isotopes.

Half-lives and the ages of rocks

Imagine a bag of microwave popcorn kernels. We can think of the popcorn kernels as unstable parent isotopes. The process of popping will symbolically represent spontaneous radioactive decay and the resulting popped popcorn will be the daughter isotopes. Though it is impossible to say when a specific kernel of popcorn is going to pop, we know how long it takes for most of the kernels to pop. There exists a relationship between number of popped kernels and amount of time passed, known as the radioactive half-life.  The half-life is the amount of time it takes for half of the sample to decay. After one half-life, 50% of the sample will have decayed (50% of the kernels will have popped). After two half-lives, the sample will be cut in half again, so that 1/4 or 25% remains. After three half-lives, 1/8 of the sample remains. This process is shown in Figure 4.

If we know the rate at which an isotope decays, we can calculate the age of a specimen given the fraction of parent and daughter isotopes in the sample. The percentage of the daughter isotope increases at the same rate as the parent isotope decreases, as shown in Figure 5.

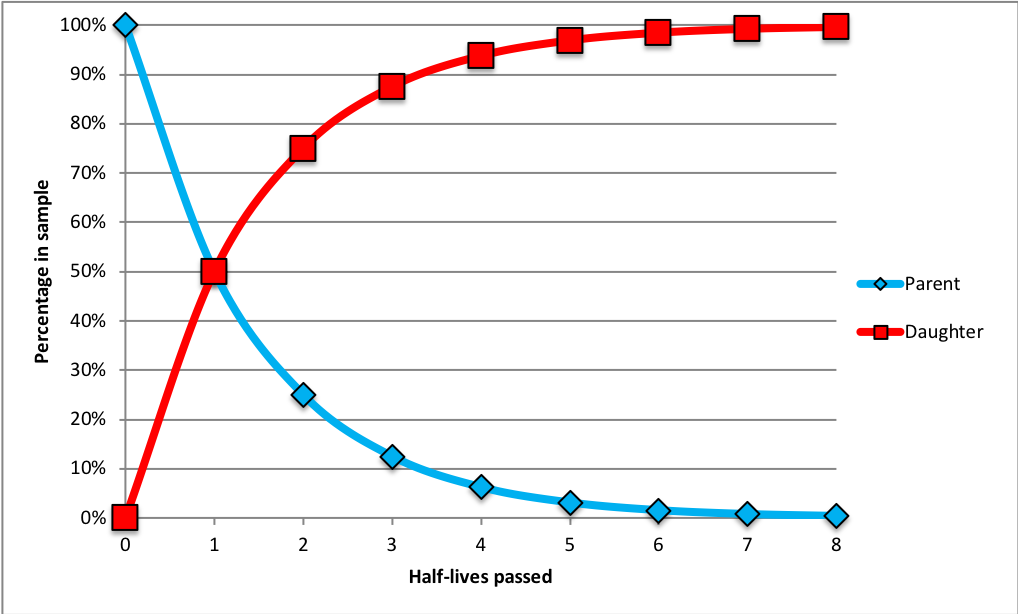
For example, suppose we analyze a rock and find that it contains 0.125 micrograms of potassium-40 and 0.875 micrograms of argon-40. What does this tell us? Potassium-40 decays into argon-40 with a half-life of 1.3 billion years, so we infer that all of the argon-40 was once potassium-40, and we started with 1 microgram: the 0.875 micrograms that is now argon-40, plus the 0.125 micrograms that remain. We know that after one half-life, 50% of the potassium-40 decays, leaving 0.5 micrograms of potassium-40 and 0.5 micrograms of argon-40. After two half-lives, another 50% decays, so 0.25 micrograms of potassium-40 remain and 0.75 micrograms have become argon-40. After three half-lives, 1/8 of the sample has decayed, leaving 0.125 micrograms of potassium-40. 7/8 of the sample is now argon-40, or 0.875 micrograms. Our rock is therefore three half-lives old: 3 [latex]\times[/latex] 1.3 billion years = 3.9 billion years.

When dating rocks, the use of many different radioactive isotopes gives even more information about the age of a specimen. The choice of isotopes depends largely on what is present in the rock sample and what is a sensible choice, given the relative half-lives of the different isotopes.  Half-lives can range from fractions of a second to billions of billions of years. Elements with longer half-lives are more useful for dating older rocks. Isotopes with half-lives comparable to the age of the substance being dated are ideal.

Statistical uncertainty

The accuracy of radiometric dating can be hard to ensure because the method depends on knowing both how much of the parent isotope was initially present, and how much of the daughter product is the result of decay. It is possible that the daughter isotope will preferentially escape from a sample, or a contaminating source will add more of either the parent or the daughter isotope.

There are ways to improve accuracy. For example, multiple samples can be analyzed from different locations in the same rock in case one area suffered contamination. It is also helpful to calculate the age using several different isotopes to check for consistent results. This offers some insurance against potential loss of daughter isotopes since contamination or loss of daughter isotopes should behave differently. Counting accuracy is improved when there is a relatively high concentration of both the parent and daughter isotope.

Even with the best laboratory practices, radiometric dating depends inherently on the type of rock. Sedimentary rocks and metamorphic rocks are not good for radiometric dating. Sedimentary rock is made up of a conglomeration of the particles eroded from different types and ages of rock. Metamorphic rock undergoes too much change. Radiometric dating is only secure for igneous rocks that remain stable. Even so, radiometric dating of igneous rocks gives only the time since they last melted.

How Old is the Earth?

Radiometric dating has enabled us to date rocks that are nearly 4 billion years old. However, the Earth itself is older than this: the early Earth was in a molten state, and no rocks from this time have survived unchanged. To determine the age of the Earth and the other planets, we use radiometric dating of meteorites. Recall from the nebular model for the formation of the solar system that these are the unprocessed debris left over from planet formation. Their ages are therefore the age of the solar system itself. From radiometric dating of the oldest meteorites, we find that the solar system began to form 4.567 billion years ago. By dating moon rocks, we find that the Earth and Moon had formed by about 4.5 billion years ago.

Review Questions

Summary Questions